Problème  suspendu :

 

-On sait que : sin()

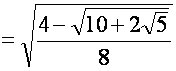
-Et si on peut calculer sin(),alors on pourra calculer sin(),  puisque :

Sin()=sin()=sin()cos()-cos()…etc

Puis, on pourra calculer les sinus de tous les angles du au

-Alors l`une des 3 racines de l`équation suivante: ,c`est :  2sin(),  mais la résolution de cette équation nous  donne :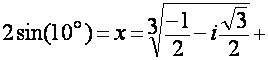

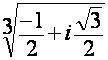
-Mais ça inutile!, à cause de la présence de l` élément «i » sous la racine cubique dans l`expression du sin() ; en sachant que toutes les racines de cette équation sont réelles

-        Alors la présence de l`élément « i » sous une racine carré ne pose aucun problème parce qu`on sait bien que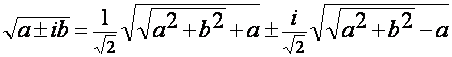 

C`est-à-dire qu`on peut toujours faire sortir le « i »de dessous d`une racine carré, mais malheureusement on ne peut jusqu`à présent le  faire en cas d`une racine cubique, sauf en utilisant les fonctions:

sin ,cos ,arctan…

dans C{corps des nombres complexes}ce qui va nous tomber dans un cercle vicieux

-On voit donc que l`unique problème qui nous a empèché de calculer sin(),c`est  la présence de l`élément « i » sous une racine cubique !

            Prochainement

_________________________________